Variance - Draft

Overview

Variance is a quantitative measurement of the spread of a set of data around the mean of the data.

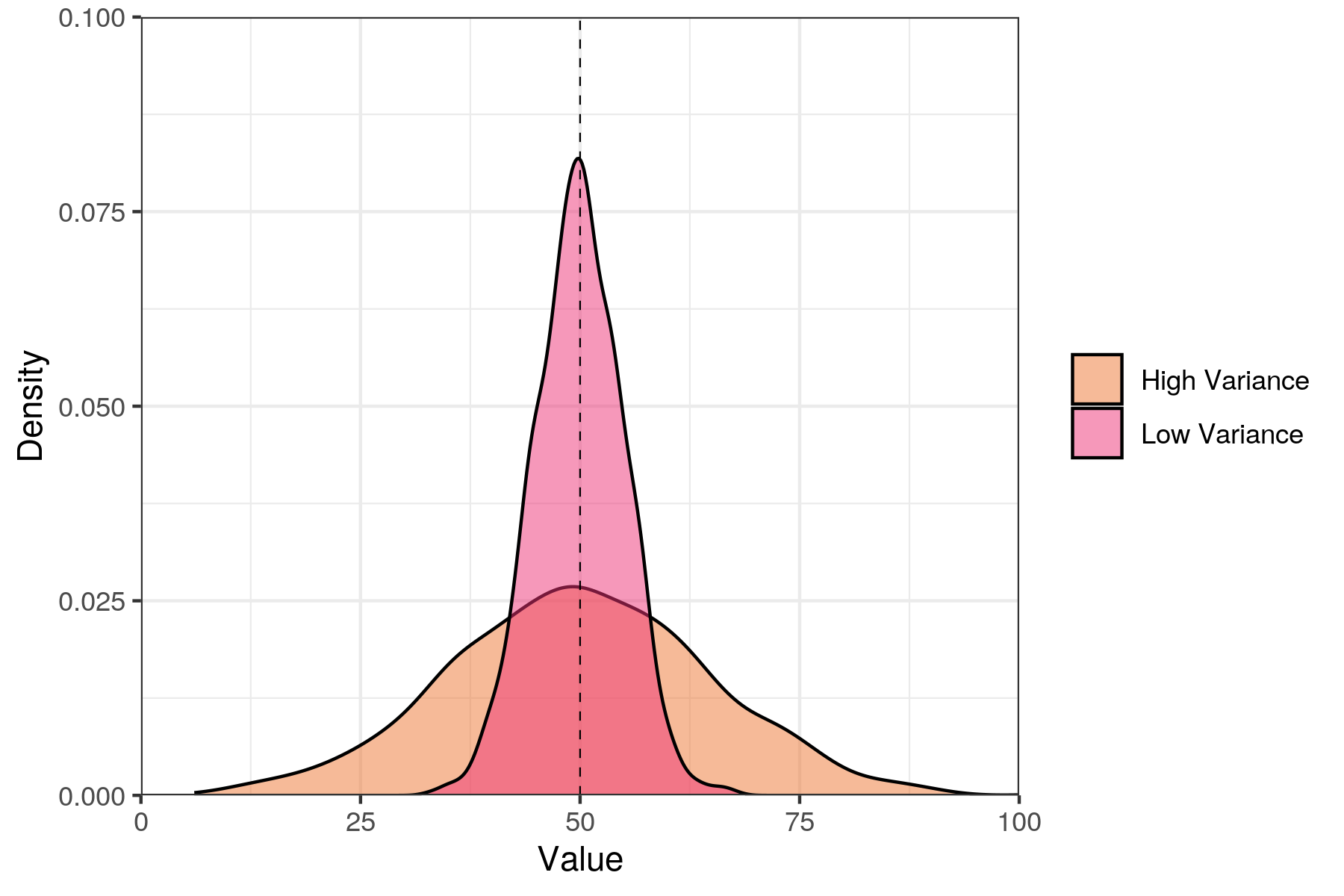
We can use variance to describe the two different distributions shown in the figure below. The orange distribution has a larger variance than the red distribution because the sample data are more spread out around the mean.

Varying Distributions

There are two formal ways to define variance. Emperically, variance describes the distribution of observed data collected from a sample or population. Theoretically, variance describes the probability distribution of a random variablea.

aRandom variables are functions that map sample spaces (e.g., \(\{ H, T \}\) is the sample space of a coin flip) to a measurable space (e.g., \(\{ H: 0, T: 1 \}\)). By definition, a random variable generates values that vary randomly1,2.

In this article, we’ll review the relationship between the two definitions of variance, but we’ll focus on the empirical definition. We’ll also discuss how variance is calculated and how it can be used to describe the spread of data.

Calculating Variance

Construction in progress…

References

1. Wikipedia. (2024). Random variable — Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Random%20variable.
2. 3.1 - Random Variables STAT 500. (2024). https://online.stat.psu.edu/stat500/lesson/3/3.1
Back to top